NeuralEE¶
- Free software: MIT license
- Documentation: https://neuralee.readthedocs.io.
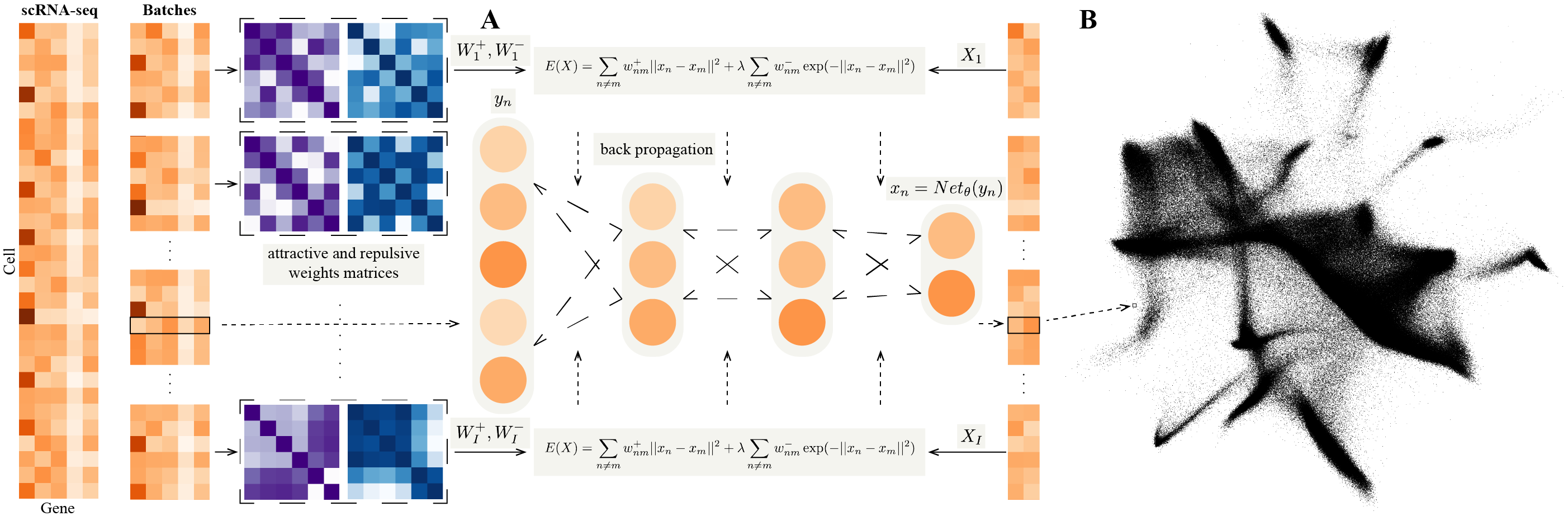
This is an applicable version for NeuralEE.
- The datasets loading and preprocessing module is modified from scVI v0.3.0.
- Define NeuralEE class and some auxiliary function, mainly for cuda computation, except like entropic affinity calculation which is quite faster computed on cpu.
- General elastic embedding algorithm on cuda is given based on matlab code from Max Vladymyrov.
- Add some demos of notebook helping to reproduce.
Installation¶
- Install Python 3.7.
- Install PyTorch. If you have an NVIDIA GPU, be sure to install a version of PyTorch that supports it. NeuralEE runs much faster with a discrete GPU.
- Install NeuralEE through pip or from GitHub:
pip install neuralee
git clone git://github.com/HiBearME/NeuralEE.git
cd NeuralEE
python setup.py install --user
How to use NeuralEE¶
- Data Loading
Our datasets loading and preprocessing module is based on scVI v0.3.0. How to download online datasets or load generic datasets is the same as scVI v0.3.0.
For example, load the online dataset CORTEX Dataset, which consists of 3,005 mouse cortex cells profiled with the Smart-seq2 protocol.
To facilitate comparison with other methods, we use a filtered set of 558 highly variable genes as the original paper.
from neuralee.dataset import CortexDataset
dataset = CortexDataset(save_path='../data/')
dataset.log_shift()
dataset.subsample_genes(558)
dataset.standardscale()
Load the h5ad file for BRAIN-LARGE Dataset, which consists of 1.3 million mouse brain cells and has been already preprocessed and remained by 50 principal components.
from neuralee.dataset import GeneExpressionDataset
import anndata
adata = anndata.read_h5ad('../genomics_zheng17_50pcs.h5ad') # Your own local dataset is needed.
dataset = GeneExpressionDataset(adata.X)
For other generic datasets, it’s also convenient to use GeneExpressionDataset to load them.
- Embedding
There are a number of parameters that can be set for the NeuralEE class; the major ones are as follows:
d: This determines the dimension of embedding space, with 2 being default.lam: This determines the trade-off parameter of EE objective function. Larger values make embedded points more distributed. In general this parameter should be non-negative, with 1.0 being default.perplexity: This determines the perplexity parameter for calculation of the attractive matrix. This parameter plays the same role ast-SNE, with 30.0 being default.N_small: This determines the batch-size for the stochastic optimization. Smaller value makes more accurate approximation to the original EE objective function, but needs larger computer memory to save the attractive and repulsive matrices and longer time for optimization. It could be inputted as integer or percentage, with 1.0 being default, which means not applied with stochastic optimization. we recommend to use stochastic optimization when only necessary, such as onBRAIN-LARGEDataset, which is hard to save the original attractive and repulsive matrices for a normal computer, and if not with stochastic optimization, it could run out of memory.maxit: This determines the maximum iteration of optimization. Larger values makes embedded points stabler and more convergent, but consumes longer time, with 500 being default.pin_memory: This determines whether to transfer all the matrix to the GPU at once if a GPU is available, withTruebeing default. If it’sTrue, it could save lots of time of transferring data from computer memory to GPU memory in each iteration, but if your GPU memory is limited, it must be set asFalse, for each iteration, the matrices of the current iteration are re-transferred to the GPU at the beginning and freed at the end.
The embedding steps are as follows:
a). Calculate attractive and repulsive matrices for the dataset.
If EE and NeuralEE without stochastic optimization will be used, it could be calculated as:
dataset.affinity(perplexity=30.0)
Or NeuralEE with stochastic optimization will be used, for example, 10% samples for each batch, it could be calculated as:
dataset.affinity_split(perplexity=30.0, N_small=0.1, verbose=True)
# verbose=True determines whether to show the progress of calculation.
b). Initialize NeuralEE class.
import torch
# detect whether to use GPU.
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
NEE = NeuralEE(dataset, d=2, lam=1, device=device)
c). Embedding.
If EE will be used, it could be calculated as:
results_EE = NEE.EE(maxit=50)
If NueralEE will be used, it could be calculated as:
results_NeuralEE = NEE.fine_tune(maxit=50, verbose=True, pin_memory=False)
For reproduction of original paper’s results, check at Jupyter notebooks files.
Computer memory consuming¶
Computer memory is mainly allocated for saving attractive and repulsive matrices, which is approximately calculated as follows:
Hyper-parameters selection of NeuralEE on large-scale data is limited on computers with limited memory.
Examples¶
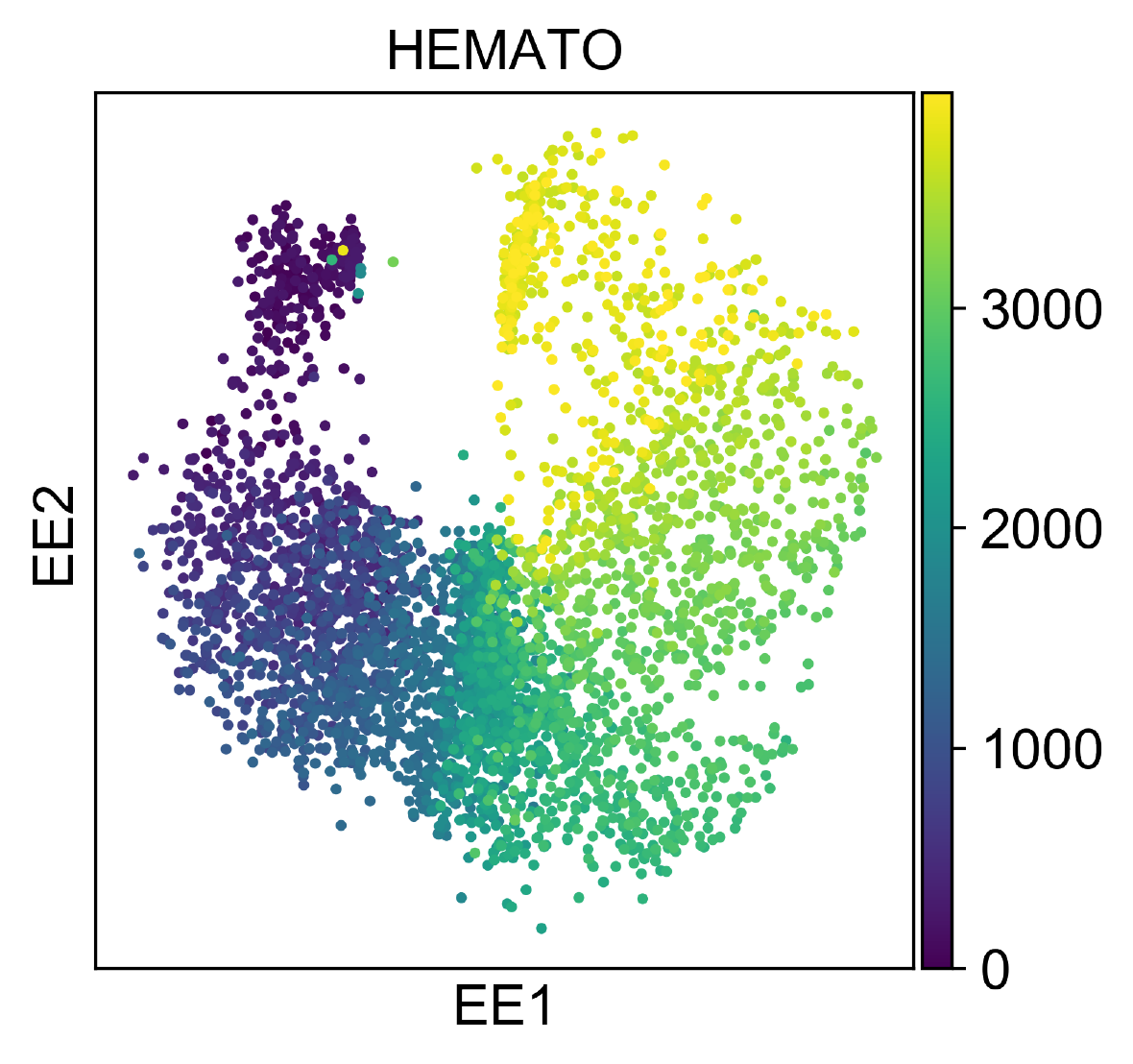
HEMATO
HEMATO Dataset includes 4,016 cells, and provides a snapshot of hematopoietic progenitor cells differentiating into various lineages.
This dataset is quite small, so we directly apply NeuralEE.EE and with (lam =10, perplexity =30).
And it could finish in several minutes on CPU, and in several seconds on GPU.
RETINA
RETINA Dataset includes 27,499 mouse retinal bipolar neurons. Cluster annotation is from 15 cell-types from the original paper.
Size of this dataset is moderate, and EE on CPU could finish in several hours.
However, NeuralEE on a normal GPU, equipped with 11G memory, without stochastic optimization could finish in almost 3 minutes.
And on a GPU of limited memory, NeuralEE with (N_small =0.5, pin_memory = True) could finish in almost 2 minutes.
The follow embedding shows the result of NeuralEE with (lam =10, perplexity =30, N_small =0.5, pin_memory = True).
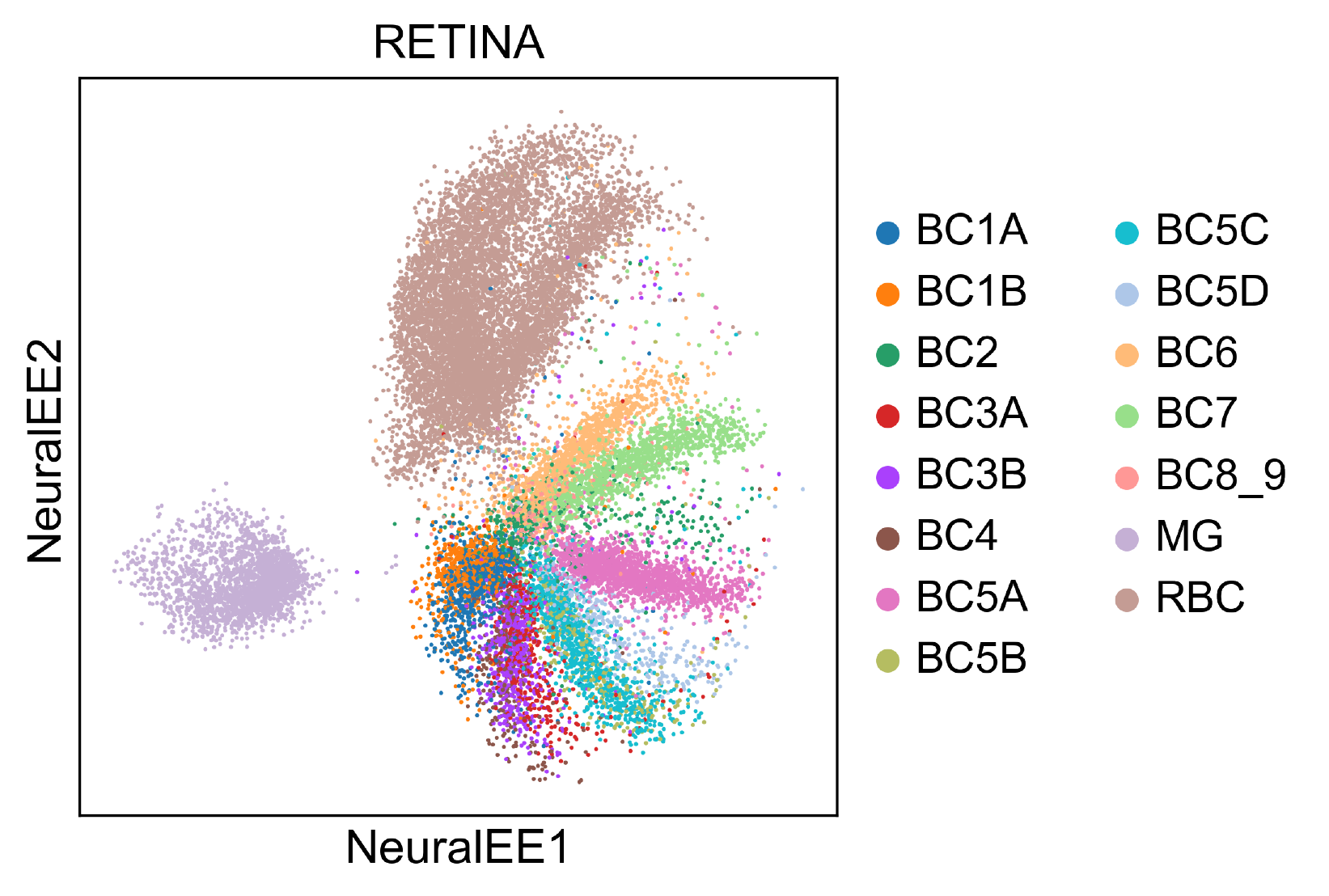
To reproduce this, check at Jupyter notebook for RETINA dataset.
BRAIN-LARGE
BRAIN-LARGE Dataset consists of 1.3 million mouse brain cells, and it’s clustered by Louvain algorithm.
This dataset is quite large, so it’s very difficult to apply EE.
Instead, we apply NeuralEE with (lam =1, perplexity =30, N_small =5000, maxit =50, pin_memory = False) on a normal GPU, equipped with 11G memory
(when set pin_memory as False, It also works on a GPU of limited memory and only uses less than 1G memory).
It needs at least 64G computer memory to save data, and it could finish less than half hour.
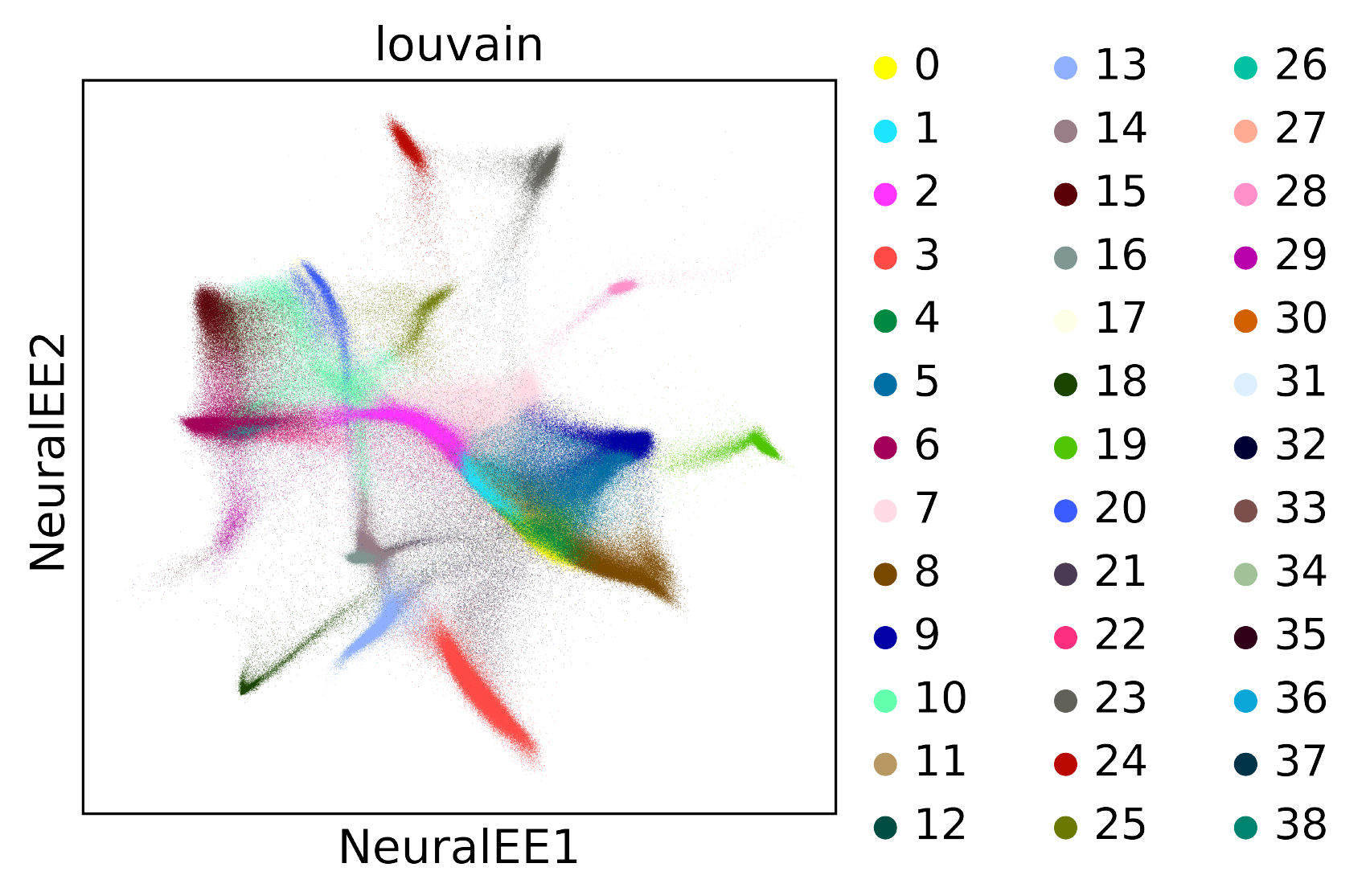
To reproduce this, check at Jupyter notebook for BRAIN-LARGE dataset.